为什么需要图神经网络
对于一个图而言,我们通常注意于三种特征:
- 整个图的特征,例如图中有多少个节点,多少条边。
- 图中节点的意义,例如对于一个图片的图表示,可能一个节点就表示了一幅图片的一个像素点。
- 图中边的意义,例如对于社交网络而言,两个节点之间有边就表示两个人是有联系的,反之则没有联系。
因此,图神经网络的任务也通常集中于这三种,我们可以分为Graph-level,Node-level以及Edge-level的任务。
如何表示一个图
无论要解决什么样的任务,首要任务肯定是要先表示出来一个图,比较容易想到的解决方案就是构造邻接矩阵。但是邻接矩阵有它的缺点,就是太过于稀疏了,我们在学Linear Algebra的时候都知道,稀疏矩阵其实是一个不好的东西,同时对于我们计算机而言,稀疏矩阵同时占用了大量没用的内存,这对于我们以后的计算肯定是会降低性能的,所以我们这里可以采用构建邻接表的形式来表示一个图。
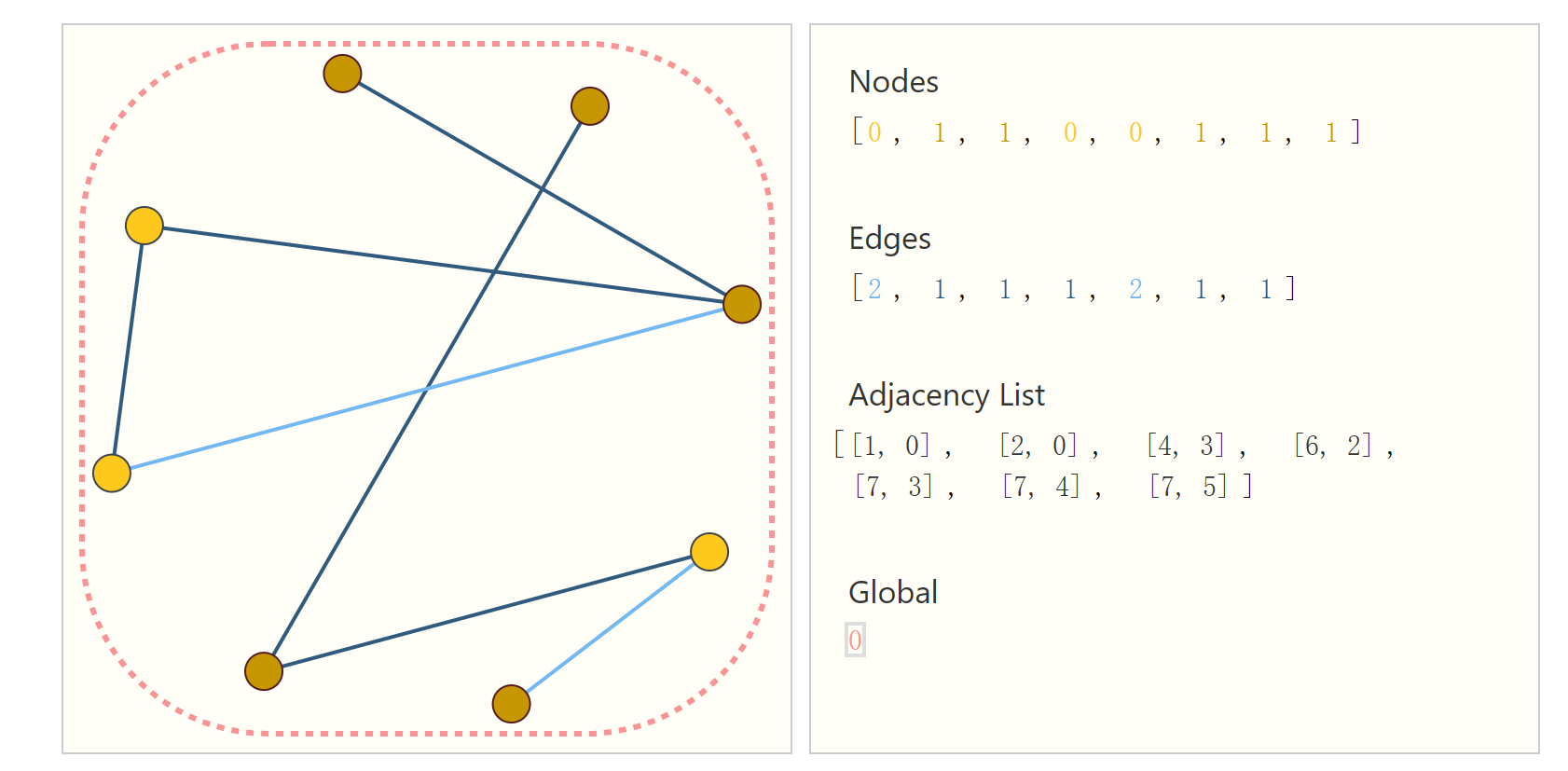
如下图所示,这样我们就可以很优雅的表示一个图了。
图神经网络结构
解决了图的表示的问题之后,我们就要开始着手设计搭建图神经网络了。首先我们考虑最简单的情况,不考虑节点之间的联系,一种最简单的方法就是,对每一个节点,我们都放到网络里面遍历一遍进行运算得到输出。同理,也可以这样对待每一条边,以及整体图形的属性都可以进行一个遍历得到结果。
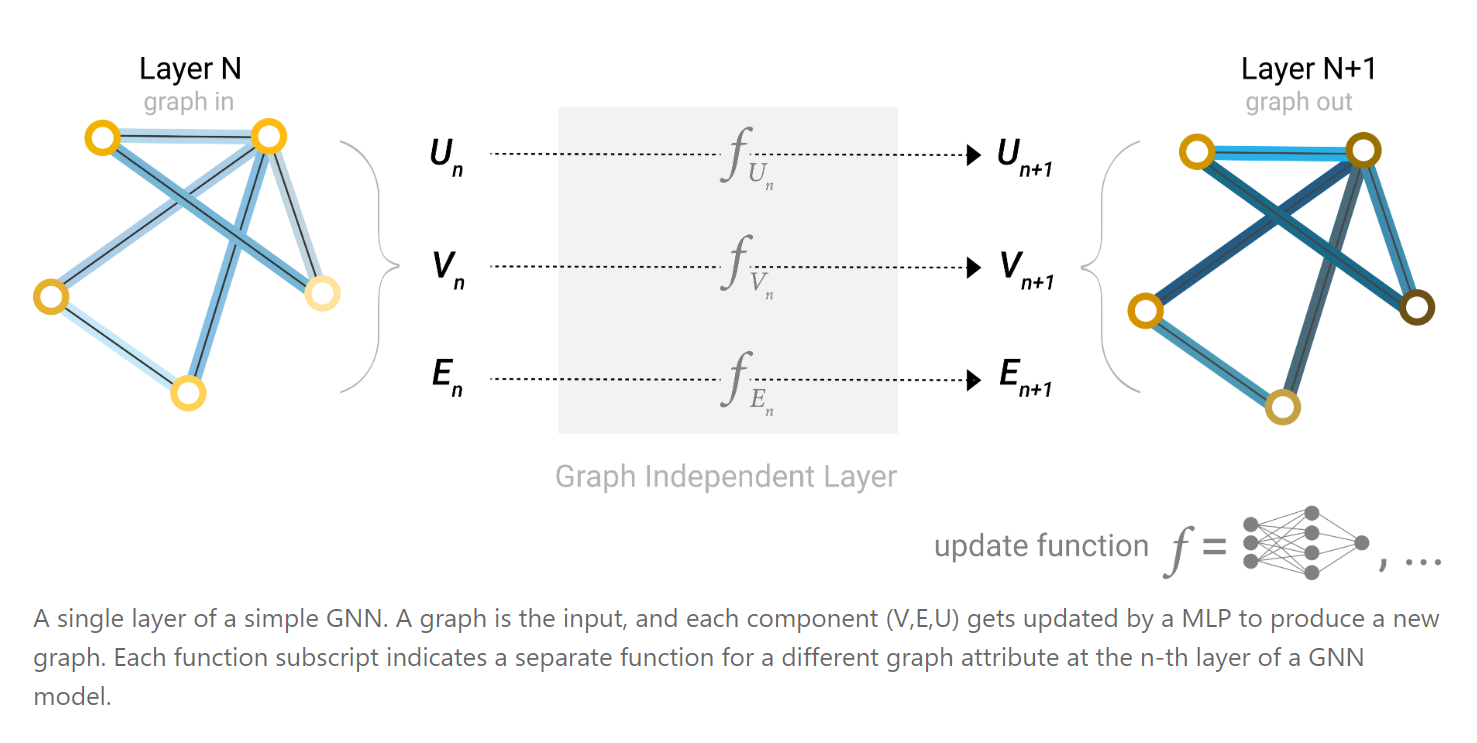
同时,由于如果我们只是单纯的使用节点或单纯使用边的信息的话,效果显然不会很好。我们可以采取pooling技术。就是将边的信息映射到点上,反之亦然。见下图:
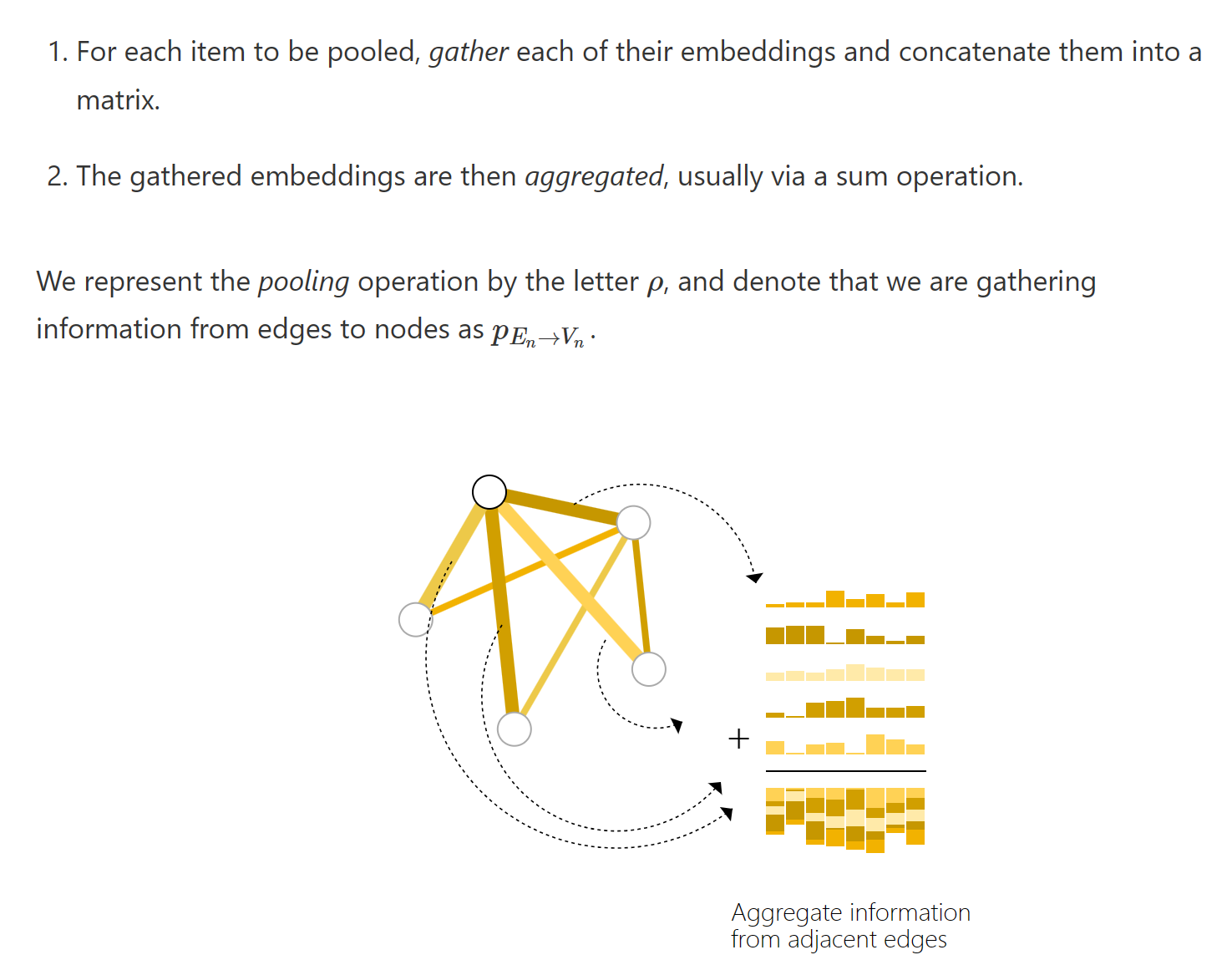
其实挺好理解的,就是把信息给融合在了一起。一般而言,我们会在上面的一层层图神经网络之后采用这样的final layer来进行分类或者回归任务。
但是我们也知道这种情况肯定效果不太好,因为我们提出图神经网络的一个重要原因就是我们要研究图中每一块每一块之间的关系,因此,一种叫做message passing的方法被提出,工作原理和上面的pooling其实差不多,只是它是在网络之间综合了邻居的所有信息,然后把它们concat起来,最后放到一个神经网络里面来进行更新。
这种方法其实有点像传统cv里面卷积的概念,例如我们对于一个像素点而言,卷积就是让它来感知它附近像素点的内容,从而达到一个特征提取的效果。在这里,同样的,对于每一个节点而言,我们能够通过多层的网络,使得一个节点能够了解到不仅仅是自己邻居节点的内容,所以这种网络结构叫做Graph Convolution Network(GCN)。
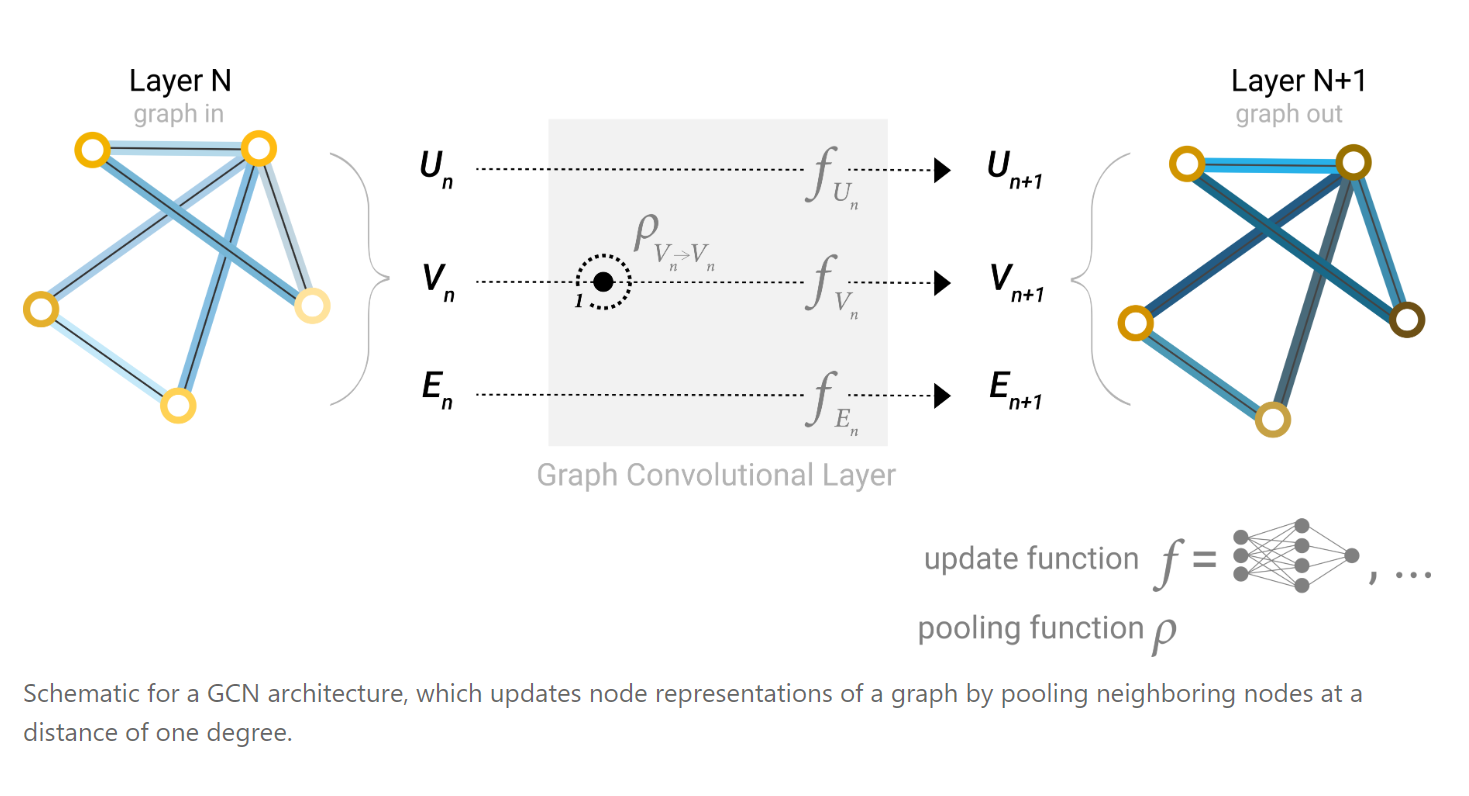
同样的,对于边而言,我们也可以用上面的message passing的方法进行信息的融合,但是可以更加的多变,如下:
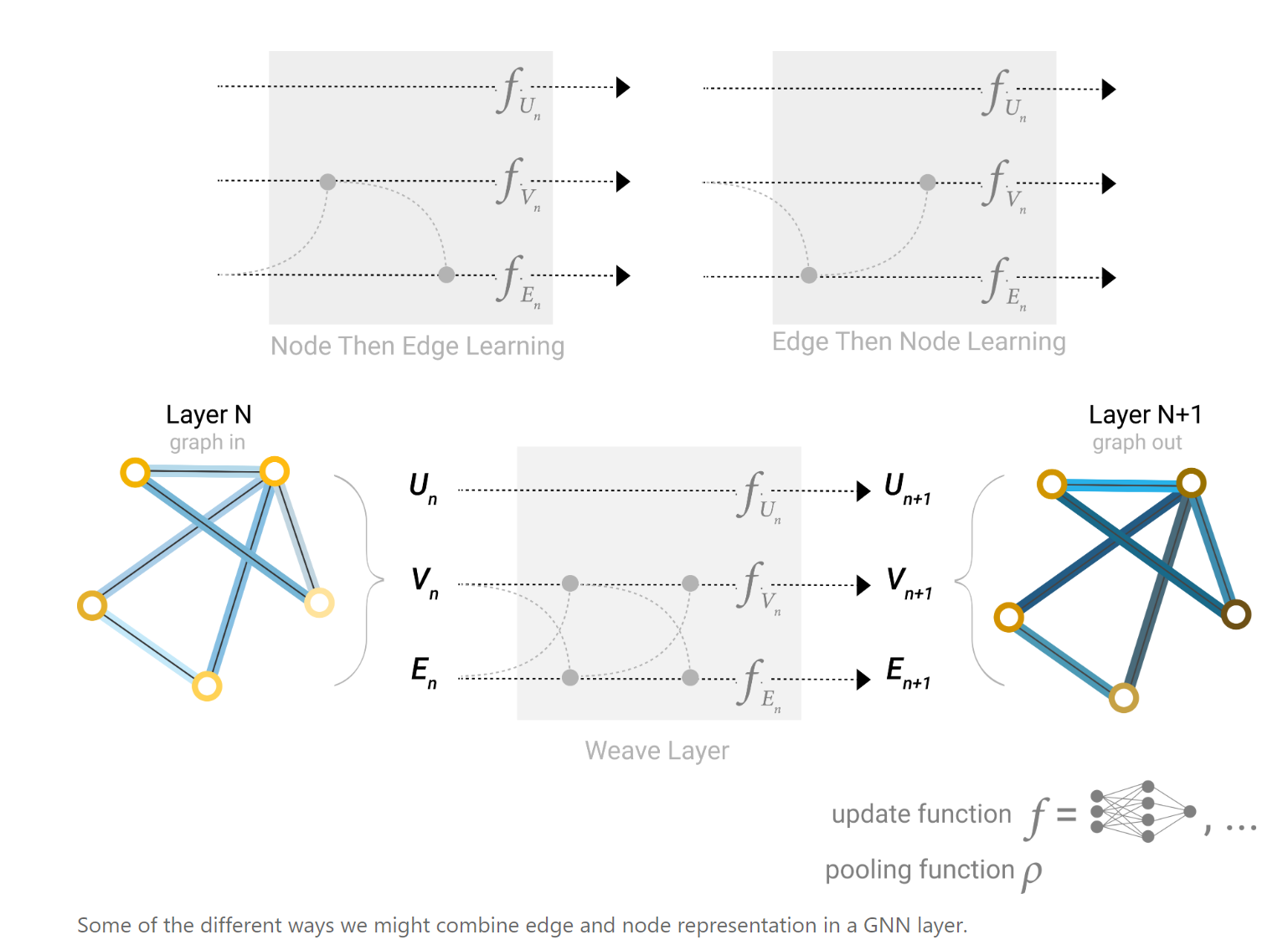
如果图过于庞大,则对于两个距离较远的节点,可能要经过很多层才能了解到对方的信息,这样信息可能就被稀疏了;另外,如果我们的任务是需要用到距离较远的节点或边或节点块,这样一步一步的传播方式显然会是效果大打折扣。因此,我们可以采用一个master node or (context vector)的方式,来代表我们的全局信息。
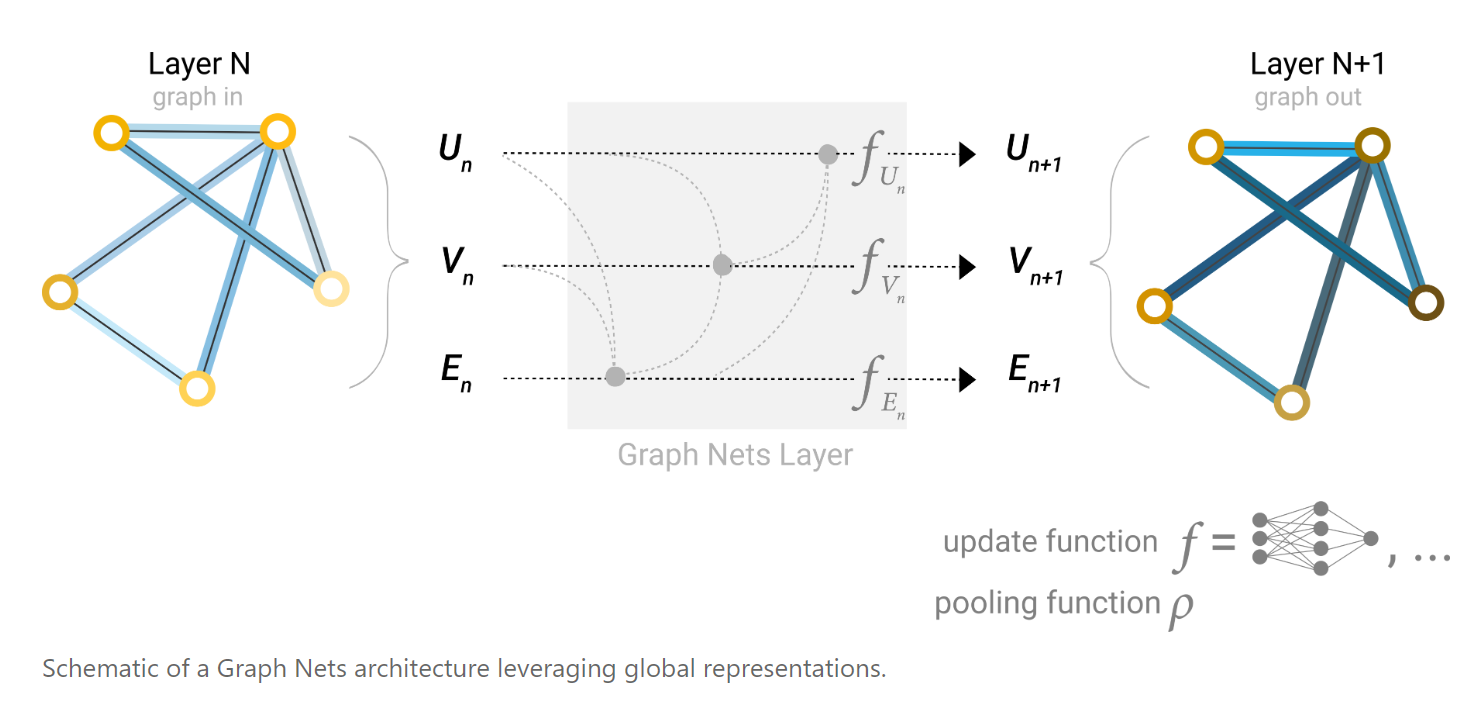
所以根据图神经网络的结构来看,有一些可以调整的超参数,例如图神经网络层数(参数数量),聚合函数类型,消息传递的方式(节点到边,边到节点,etc.)通过实际任务来进行参数的调整。
杂项与后续
特殊的图
我们在上面构造图的时候,都是使用最简单的构造方式,但在实际应用中,我们可能需要不同种类的图,例如我们有多图、超图、超节点、层次图等等,我们也需要图神经网络来对这种图来进行预测和训练。
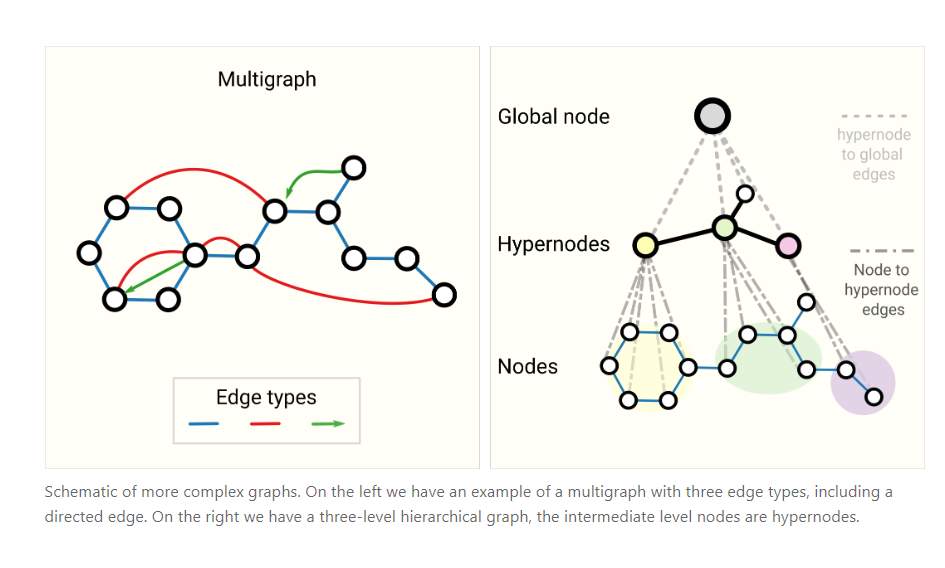
貌似这里就可以用超图来做生信?比如其中的一个超节点就可以表示一个苯环🤨
采样方法
在训练图片或者文本的时候,我们通常是对于所有的训练集进行一定额度的批量采样(batch),部分的进行训练。最后计算loss,然后更新参数,再在下一个batch下进行训练。
对于图而言,显然我们不能这样的训练,我们能做的就是选取一个一个的子图,在这些子图上面进行训练。这样对于我们选取多远的邻居就有一定的难度。例如我们选的太近可能会导致视野太窄,选的太远有又可能会有信息消失或者稀疏等情况出现。有一些方法来选择我们需要的子图:
如果我们希望保留邻域级别的结构,一种方法是随机抽取一定数量的节点,即我们的节点集。然后添加与节点集相邻的距离为 k 的邻接节点,包括它们的边。每个邻域可视为一个单独的图,GNN 可在这些子图的批次上进行训练。由于所有相邻节点的邻域都不完整,因此可以掩盖损失,只考虑节点集。
更有效的策略可能是先随机抽样一个节点,将其邻域扩大到距离 k,然后在扩大的集合中挑选其他节点。一旦构建了一定数量的节点、边或子图,就可以终止这些操作。如果情况允许,我们可以通过选取一个初始节点集,然后对一定数量的节点进行子采样(例如随机采样,或通过随机漫步或 Metropolis 算法)来构建恒定大小的邻域。
选取聚合函数
我们在进行边和节点的信息融合的时候,通常需要选择合适的聚合函数来进行消息传递。例如求和,取最大值,取平均等等,这也需要我们根据具体情况来选择。
边与节点
(PS:笔者的离散数学学的很差,可能这里写的会有一些错误)
我们针对图上边的某些特点做预测的时候,往往可以把边转化为节点来进行操作,这里我们可以使用对偶图来进行操作。
通常我们对节点的操作要比对于边的操作要容易一些,因此我们使用对偶图的性质来把问题作为转化,使其进行简单化。
Attention is all you need(GAT)
相同于NLP中的注意力机制,我们在GNN中也有这样的注意力机制。对于某一些任务,可能我们只是想侧重于某一些特定的节点,只需要他们的特征,这里我们就可以在其中加一个attention机制。这种图神经网络机制叫做GAT。
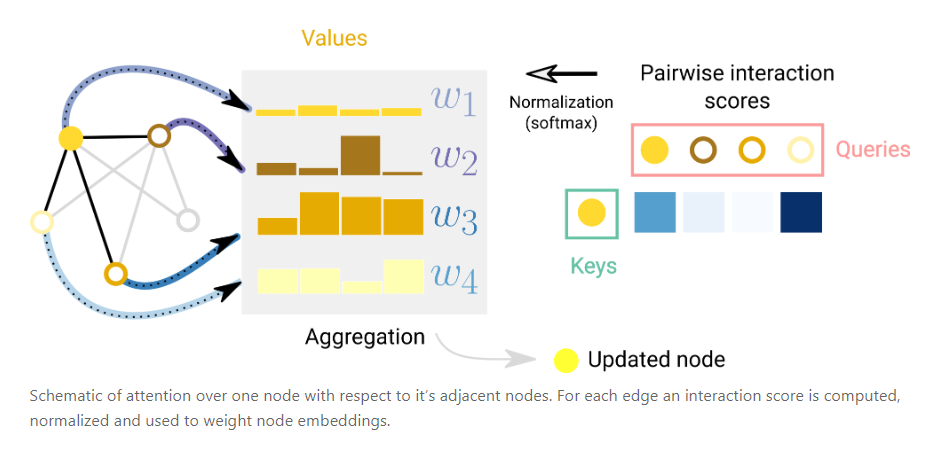
参考文献
本文参考网站GNN入门。